BẬT MÍ cách giải bất phương trình mũ và logarit

Bất phương trình mũ và logarit là một chuyên đề quan trọng trong toán học 12. Vậy bất phương trình mũ và logarit có dạng thế nào? Cách giải bất phương trình mũ và logarit ra sao? Hãy cùng Bankstore.vn khám phá qua nội dung bài viết sau này nhé.

Toán 12 Bài 6: Bất phương trình mũ và bất phương trình lôgarit | HỌC247

👉 Tải App HOC247 cho iOS/Android: http://onelink.to/4nuchu

Phần 1: BẤT PHƯƠNG TRÌNH MŨ

Bạn đang xem: BẬT MÍ cách giải bất phương trình mũ và logarit

1. Giải bất phương trình mũ bằng phương pháp đưa về cùng cơ số [00:18]

2. Giải bất phương trình mũ bằng phương pháp logarit hóa [13:29]

3. Giải bất phương trình mũ bằng phương pháp đặt ẩn phụ [27:03]

4. Giải bất phương trình mũ bằng phương pháp hàm số [50:17]

Phần 2: BẤT PHƯƠNG TRÌNH LÔGARIT

1. Giải bất phương trình lôgarit bằng phương pháp đưa về cùng cơ số [01:06:37]

2. Giải bất phương trình lôgarit bằng phương pháp mũ hóa [01:21:37]

3. Giải bất phương trình lôgarit bằng phương pháp đặt ẩn phụ [01:41:08]

4. Giải bất phương trình lôgarit bằng phương pháp hàm số [02:01:02]

Cảm ơn các em đã xem Video bài giảng Giải tích 12 Chương 2 Bài 6 của TS Phạm Sỹ Nam về Bất PT Mũ và Bất PT Lôgarit.

————————–

👉 Học trọn khóa: http://bit.ly/luyen-thi-THPTQG-Toan

————————–

Theo dõi HỌC247 tại:

👉 Facebook: http://bit.ly/FBHoc247

👉 Youtube: http://bit.ly/hoc247tv

Xem thêm : Tổng Hợp Hơn 300 Mẫu Áo Dài Phụ Nữ Việt Nam

👉 Website: https://hoc247.net/

👉 App iOS: http://bit.ly/AppHoc247iOS

👉 App Android: http://bit.ly/AppHoc247and

————————–

Mong được sát cánh cùng các em học sinh

Trân trọng!

© Copyright by HỌC247 ❌ Do not Reup ❌

Bất phương trình mũ và logarit

Bất phương trình mũ

Ở dạng cơ bản, bất phương trình mũ có dạng:

ax > b (hoặc ax <b, ax ≥ b, ax ≤ b) với a > 0 và a ≠ 1.

Xét phương trình dạng ax > b:

• Nếu b ≤ 0 thì phương trình ax > b có tập nghiệm là R.
• Nếu b > 0 và a > 1 thì ax > b khi và chỉ khi x > logab
• Nếu b > 0 và a < 1 thì ax > b khi và chỉ khi x < logab

Bất phương trình logarit

Ở dạng cơ bản, bất phương trình logarit có dạng:

logax > b (hoặc logax < b, logax ≤ b , logax ≥ b) với a > 0 và a ≠ 1.

Xét phương trình logax > b :

• Với a > 1 ta có logax > b khi và chỉ khi x > ab
• Với 0 < a < 1 ta có logax > b khi và chỉ khi 0 < x < ab

>> Xem thêm: Phương trình mũ, Phương trình logarit là gì? Phương pháp giải phương trình mũ và logarit

Định lý về bất phương trình mũ và logarit

Với chuyên đề về bất phương trình mũ và logarit, ta cần nhớ 2 định lý sau:

• Định lý 1: Bất phương trình af(x) < aφ(x) với 0vàlt; a <1 tương đương với bất phương trình f(x) >φ (x); còn với a > 1 thì tương đương với bất phương trình f(x) < φ(x). {af(x) < aφ(x) 0 < a <1 f(x) > φ(x) {af(x) < aφ(x) a >1 f(x) < φ(x)
• Định lý 2: Bất phương trình loga f(x) < loga φ(x) với o < a < 1 tương đương với hệ bất phương trình {f(x) > φ(x) φ(x) >0 ; còn với a >1 thì tương đương với hệ bất phương trình {f(x) < φ(x) f(x) >0. Với bất phương trình dạng loga f(x) >c và a f(x) > d (d > 0) có thể đưa về dạng ở hai định lý trên bằng phương pháp dùng c = loga ac , d = ad .

Sau khoản thời gian đã nắm rõ hai định lý này, tất cả chúng ta hãy cùng tìm hiểu cách giải bất phương trình mũ và logarit nhé.

Cách giải bất phương trình mũ và logarit

Dạng 1: Dạng cơ bản

Cách giải một bất phương trình mũ đơn giản như các giải một phương trình mũ đơn giản, ta có thể đặt ẩn phụ hoặc đưa về cùng cơ số…

Xem thêm : Tổng Hợp Các Mẫu Thông Báo Nghĩ Lễ Hay Dùng

Ngoài ra, ta có thể logarit hóa, đưa về dạng bất phương trình mũ logarit và đặt các ĐK để phương trình có nghiệm. Sau khoản thời gian tìm được kết quả cần so sánh với ĐK để Kết luận nghiệm thích hợp.

Ví dụ: Giải bất phương trình: 32x+5 3x+2 + 2

Nhận xét rằng 32x+5 = 3. 32(x+2) . Đặt 3x+2 = t (t > 0) đi đến bất phương trình

3t2 – t – 2 ≤ 0. Giải BPT này tìm được -23 ≤ t ≤1. Từ đó: {3x+2-23 3x+2 ≤ 3 khi và chỉ khi x ≤ -2

Với một bất phương trình logarit, ta cũng đưa về cùng cơ số Theo phong cách đưa về cùng cơ số:

• Với a > 1 ta có loga f(x) > loga g(x) khi và chỉ khi g(x) > 0 và f(x) < g(x).
• Với 0 < a <1 có loga f(x) > loga g(x) khi và chỉ khi thỏa mãn đồng thời 2 ĐK: g(x) > 0 và f(x) < g(x).

Đồng thời ta cũng có thể có thể giải bằng phương pháp đặt ẩn phụ.

Dạng 2: bất phương trình mũ và logarit có chứa tham số

Đây là một dạng về bất phương trình mũ và logarit khó. Với dạng bài này, ta có thể đặt ẩn phụ để triệt tiêu tham số hoặc sử dụng tính đơn điệu của hàm số và kẻ bảng biến thiên.

Ví dụ: Tìm tất cả những giá trị của tham số a để cho BPT sau có nghiệm:

loga+x x(a-x)< loga+x x

Hướng dẫn:

Với những ĐK: x > 0, a+x > 0, a – x > 0, a + x ≠ 1 thì BPT trên tương đương với BPT loga+x (a-x) < 0.

BPT có nghiệm nếu thỏa mãn hệ ĐK:

{xvàgt;0 xvàgt;-a xvàgt;a a+xvàgt; 1 a-xvàlt;1 hoặc: {xvàgt;0 xvàgt;-a xvàlt;a a+xvàlt; 1 a-xvàgt;1

Tiếp theo, ta sử dụng đồ thị để xác định tập nghiệm của bất phương trình.

Để tìm hiểu thêm về các dạng bài tập, ví dụ và cách giải, tất cả chúng ta có thể tìm kiếm các bài giảng và dạng bài tập trên internet với từ khóa: bất phương trình mũ và logarit violet.

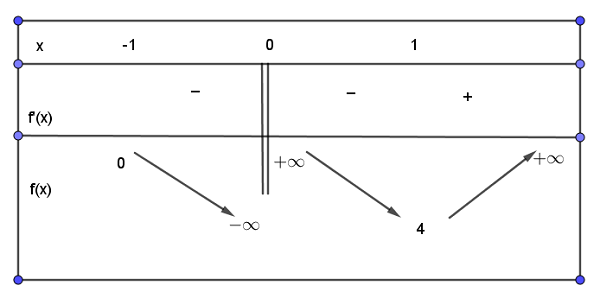
>>> Xem thêm: Bất đẳng thức là gì? Các bất đẳng thức đáng nhớ và quan trọng

Bất phương trình mũ và logarit là một chuyên đề khó trong toán học 12. Vì thế ta cần thật tập trung lúc học phần kiến thức này. Hi vọng qua nội dung bài viết trên đây, tất cả chúng ta đã hiểu bất phương trình mũ và logarit có dạng thế nào và cách giải bất phương trình mũ và logarit.

Nguồn: https://bankstore.vn
Danh mục: Tổng Hợp